Quadrados mágicos (parte I)
ORIGEM E HISTÓRIA DOS QUADRADOS MÁGICOS
“Toda a matéria de quadrados mágicos e arranjos conectados de números parece à primeira vista ocupar uma posição que é totalmente isolada dos outros departamentos de Matemática Pura. ”
Percy A. McMahon
Meu gosto pela Matemática a Geometria e o Desenho, me levou por caminhos pouco usuais. Sempre que se falava de Natureza, havia uma ligação forte com a Matemática. Pois, ela – a Matemática – está presente em todos os domínios científicos. Parte dessa combinação maravilhosa de matemática e natureza pode ser observada com os números de Fibonacci.
Mas que Matemática seria esta que abrange todas as coisas da Natureza? Galileu Galilei foi o primeiro em reparar que “O livro da Natureza está escrito em caracteres matemáticos” , isto é, que a Matemática é a linguagem das Leis Naturais, Leis Universais segundo as quais criamos e manifestamos a nossa realidade.
A primeira vez que li algo sobre o assunto foi referido aos “Quadrados Mágicos”. É aqui que encontrei a resposta ao que procurava. Na realidade o pouco que conhecemos sobre os quadrados mágicos, está sintetizado nas seguintes palavras : Não se sabe a origem dos quadrados mágicos. Há quem considera de origem indiana, há quem considera de origem chinesa e há quem acredita que sua invenção data da origem da ciência. Há quem diga que “a ciência do quadrado mágico é uma ciência inicial que Deus criou. Ele próprio iniciou Adão nesta ciência” (Jean Chevalier e Alain Gheerbrant, Dicionário de símbolos , Robert Lafron/Júpiter, Paris,1982).
Antes de iniciar o estudo da matemática dos Quadrados Mágicos (QM), e de tudo o que aprendemos sobre eles durante esses anos, ocuparemos todos de algo muito importante, sua origem, e como surgiram em nossas mentes.
Acredita-se que os chineses foram os primeiros a descobrir as propriedades dos QM e que eles chamavam de Lo Shu. A lenda conta que o imperador da antiga China, chamado Fu Hsi (3000 aC), estava meditando às margens do Rio Amarelo quando emergiu uma tartaruga – considerada um animal sagrado – com estranhas marcas no casco. Fu Hsi viu que as marcas na forma de nós, feitas num tipo de barbante, podiam ser transformadas em números e que todos somavam quinze em todas as especiais, como se fossem algarismos mágicos.
Mas meu interesse maior foi quando encontrei um trabalho sobre os QM pelo matemático Heinrich Cornelius Agrippa (1486-1535) filósofo matemático do século XVI, em sua obra “De Occulta Philosophia” desenvolve os quadrados mágicos de ordem 3, 4, 5, 6, 7, 8 e 9, conhecidos atualmente como quadrados mágicos tradicionais, sendo que todos eles começam pelo número 1. E são deles que t rataremos nesta obra (ver Quadro I)
OS QUADRADOS MÁGICOS TRADICIONAIS

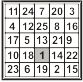
Ordem 3 Ordem 4 Ordem 5
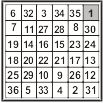
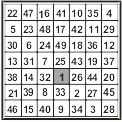
Ordem 6 Ordem 7
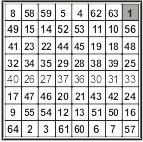
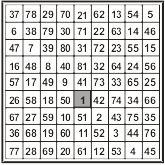
Ordem 8 Ordem 9
QUADRO I
Continuando com a pesquisa, nos fins do século XIX renova-se o interesse pelos quadrados mágicos WW Rouse Ball (1883), EM Laquière (1880), Edouard Lucas (1882) são alguns dos matemáticos que se ocuparam dos problemas de construção , classificação e enumeração de quadrados mágicos. E que de certa forma seria meu interesse também. Não existiam equações para facilitar os cálculos
Consideram-se quadrados mágicos, as composições matemáticas contidas por uma sucessão de números dispostos de tal maneira que a soma dos números que se encontram em cada fila, coluna ou diagonal, seja constante.
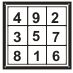
A ordem, n, de um quadrado mágico é o número de linhas ou colunas que se comporta. Assim na matriz da Fig. 1 representamos o primeiro dos sete Quadrados Mágicos (QM), ou seja, o QM de ordem 3

Figura 1
Este QM é muito interessante, pois possibilita uma reflexão de fácil entendimento. O exemplo mais simples e cuja constante de acordo com sua definição é 15, conforme mostrado a seguir:
Considerando as filas que temos:
4 + 9 + 2 = 15
3 + 5 + 7 = 15
8 + 1 + 6 = 15
Considerando as colunas que temos:
4 + 3 + 8 = 15
9 + 5 + 1 = 15
2 + 7 + 6 = 15
Considerando as diagonais temos:
4 + 5 + 6 = 15
2 + 5 + 8 = 15
E que também encerra as seguintes propriedades:
4² + 9² + 2² = 8² + 1² + 6² e
4² + 3² + 8² = 2² + 7² + 6²
E mais:
4 + 6 = 10
3 + 7 = 10
8 + 2 = 10
1 + 9 = 10
Um QM de ordem n é composto de n² números. Se estas cifras seguem a série de números naturais desde 1 até n², então o resultado (ou constante mágico) a encontrar em cada fila, coluna e diagonal se pode calcular com o seguinte o algoritmo:
S (n) = (n² + 1) xn/2 S (n) = Constante Mágica
Exemplo: QM de ordem 3 S = (3² + 1) x 3/2 = 10 x 3/2 = 30/2 = 15
Outros resultados ver tabela: para QM de várias ordens:

Esta constante não é visível à primeira vista, mas indica a posição de cada número dentro da matriz. É uma das características da Lei, ela é de forma imperceptível
mas uma vez conhecendo sua constante, também podemos saber a soma total de qualquer quadrado mágico, com o seguinte algoritmo:
St = (n² + 1) x (n²) /2 St = Soma total (ex. QM de ordem 3)
St = (3² + 1) x (3²)/2 = 10 x 9/2 = 90/2 = 45


 Dalai Lama
Dalai Lama Platão
Platão Karl Marx
Karl Marx





















uauuuuuuuuuuu
Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...Senhor de Huanca bla bla bla...